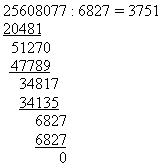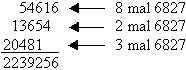Die Napierschen Rechenstäbe
Allgemein
Die Erfindung der Rechenstäbe
des schottischen Mathematikers Lord Lapier of Merchiston (1550-1617)
war für die Entwicklung in der Informatik sehr bedeutend. Napier
entwickelte im Zusammenhang mit den Rechenstäben die Logarithmen.
Napier selbst hielt seine Rechenstäbe für eher unbedeutend, so dass
er sie auch erst in ihm Jahr 1617 veröffentlichte. Die Napierschen Rechenstäbe
ermöglichten es erstmals mehrstellige Zahlen schnell und unkompliziert
zu muliplizieren. Die
quarderförmigen Stäbe besitzen auf ihren Seitenflächen
jeweils eine Kolonne des kleinen Einmaleins. Multiplikation bzw. Subtrakion
von ein- oder mehrstelligen Zahlen lassen sich durch entsprechendes
Zusammenlegen der Stäbe zu einer Addition bzw. Subtraktion vereinfachen.
Die Napierschen Rechenstäbe
wurden bis ins 19. Jahrhundert intensiv genutzt. 1620 wurde die logarithmische
Skalierung der Rechenstäbe von Prof. Edmund Gunter aufgegriffen,
dieser entwickelte daraus den Vorgänger des Rechenschiebers.
Entwicklung der Rechenstäbe
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
|
2
|
4
|
6
|
8
|
10
|
12
|
14
|
16
|
18
|
|
3
|
6
|
9
|
12
|
15
|
18
|
21
|
24
|
27
|
|
4
|
8
|
12
|
16
|
20
|
24
|
28
|
32
|
36
|
|
5
|
10
|
15
|
20
|
25
|
30
|
35
|
40
|
45
|
|
6
|
12
|
18
|
24
|
30
|
36
|
42
|
48
|
54
|
|
7
|
14
|
21
|
28
|
35
|
42
|
49
|
56
|
63
|
|
8
|
16
|
24
|
32
|
40
|
48
|
56
|
64
|
72
|
|
9
|
18
|
27
|
36
|
45
|
54
|
63
|
72
|
81
|
|
In
der Antike nutze man Multiplikationstabellen wie die Einmaleins
Tafeln (Abbildung) zur Berechnung einer Multiplikation. Bei dem
von Pythagoras (580-500 v.Chr.) entwickelten Verfahren, sucht man
die Zeile auf in der der erste Faktor steht, anschließend in den
Spalten den zweiten Faktor. Daraufhin findet man im Kreuzungspunkt
Ergebnis der Multiplikation. Für die Multiplikation von 7 x 8 ergibt
sich somit 56. Sind mehrstellige Zahlen zu muliplizieren, so werden
Teilprodukte gebildet und anschließend, entsprechend der schriftlichen
Muliplikation addiert.
|
Napiersche Rechentafel
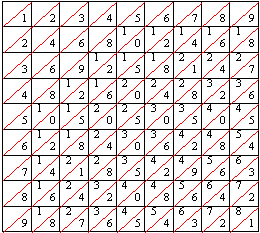 |
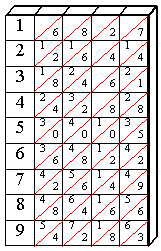
John Napier erforschte
zunächst die Multiplikation einer beliebigen natürlichen
Zahl mit einer einstelligen Zahl. Es ergab sich, dass für
diese Multiplikation allein das kleine Einmaleins benötigt
wurde. Damit das Produkt bestimmt werden kann, müssen die
Teilergebnisse richtig addiert werden. Napier veränderte
die Einmaleins Tafeln nun so, dass neben den Produkten auch die
addierenden Zahlen sofort erkennbar waren, indem der transversale
Linien und die zugehörigen Zahlen hinzufügte (Abbildung).
Anschließend trennte er die Tafel den Spalten nach und fertigte
von jedem Stab mehrere Kopien an. Damit ließen sich beliebige
Multiplikationen ausführen.
|
Multiplikation
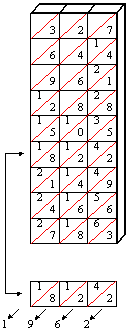 |
Ein Einstelliger Faktor
Um eine mehrstellige
Zahl mit einer einstelligen Zahl zu multiplizieren bildet man
zunächst die mehrstellige Zahl aus den Rechenstäben,
anschließend den einstelligen Faktor aus der Spalte. Damit
reduziert sich das Problem auf eine Additionsaufgabe. Möchte
man das Produkt aus 6 x 327 bestimmen, so setzt man aus den einzelnen
Stäben die Zahl 327 zusammen (Abbildung). Daraufhin geht
man in die 6. Zeile, die Zeile entspricht dem Faktor 6. Dann addiert
man von rechts nach links, die schräg übereinander stehenden Zahlen.
Daraus ergibt sich das Ergebnis 1962.
Mehrstellige Faktoren
| Zur
Muliplikation mehrstelliger Zahlen muss man einen Umweg gehen,
indem man die einzelnen Ziffern multipliziert und die Zwischenergebnisse
addiert. Beispiel: 328 x 6827 Ergebnis: 2239256 Die Rechnung
mit mehrstelligen Faktoren wird somit etwas komplizierter,
jedoch immer noch einfacher als durch schriftliche Multiplikation.
|
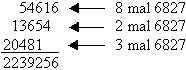 |
|
Division
 |
Die
Division ist nicht direkt mir den Napierschen Rechenstäben
ausführbar. Sie lässt sich jedoch auf den Algorithmus
der schriftlichen Division zurückführen. Dabei dienen
die Rechenstäbe der Vereinfachung von Zwischenschritten. Der
entscheidende Vorteil beim Dividieren liegt darin, dass der jeweiligen
Quotienten lediglich vergleichen werden muss. Das folgende Beispiel
soll die Arbeitsweise veranschaulichen: Zuerst legt man sich aus
den Rechenstäben den Divisor 6827. Die Produkte einzelnen lassen
sich jetzt erkennen. Das Produkt wird nun an den Divisor 25608 angenähert.
Die Zeilennummer entspricht der erster Ziffer des Quotienten. Der
erste Quotiert ergibt demnach 3. Anschließend folgt die bekannte
Rückrechnung und Differenzbildung. Darauf nimmt man die nächste
Ziffer aus dem Dividenden und setzt den Algorithmus, wie beschrieben
fort.
|
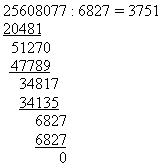
|